LSTM是一种结构被精心设计过的一种RNN，它的参数更新和普通的BP算法有一些区别，即所谓的truncated back propagation，相关论文里公式推导的不是特别详细会跳过一些步骤，而且不同文章里用的表示符号又不尽相同，网上 似乎也没有找到一个特别完整的推导，所以我写下这篇文章记录下推导过程，尽可能把过程的细节都写清楚，如果能顺便帮到别人也好：）

Note:本文仅涉及LSTM（不含Peephole）的参数更新算法的推导介绍，并不涉及对于LSTM原理的介绍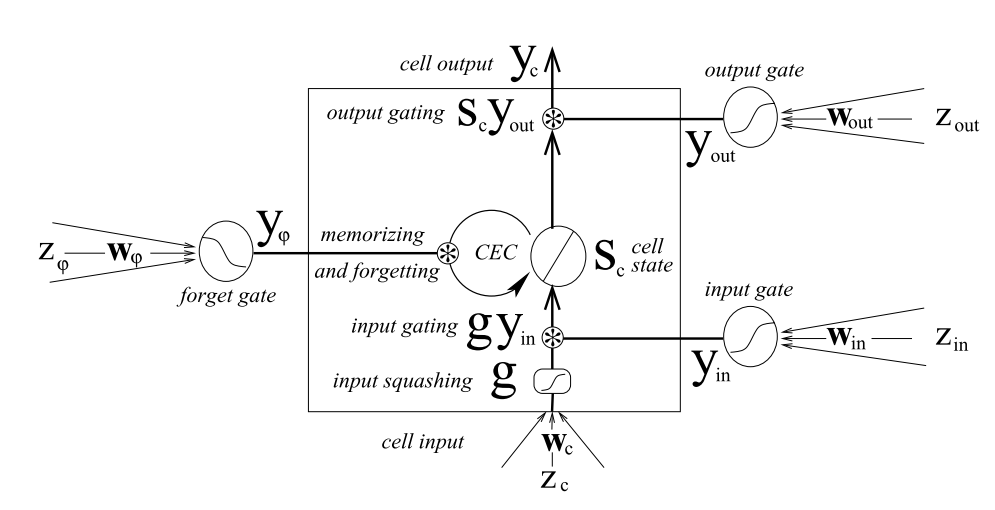

  上图即使LSTM的一个memory block，对照上图，首先展示LSTM的forward pass：

ceil input 部分

$$z_{ {c_j}}(t) = \sum_m{w_{ {c_j}m}y_m(t-1)}$$

其中$c_j$表示，memory ceil的第j维，t代表RNN中的时刻$w_{ {c_j}m}$表示y(t-1)的第m维连接memory ceil的第j维的权重

input gate部分

$$y_{in_j}(t) = f_{in_j}(z_{in_j}(t)),\qquad z_{in_j}(t) = \sum_m{w_{ {in_j}m}y_m(t-1)}$$

forget gate部分

$$y_{\varphi_j}(t) = f_{\varphi_j}(z_{\varphi_j}(t)),\qquad z_{\varphi_j}(t) = \sum_m{w_{ {\varphi_j}m}y_m(t-1)}$$

cell state部分

$$s_{c_j}(t) = y_{\varphi_j}(t)s_{c_j}(t-1) + y_{in_j}(t)g(z_{ {c_j}}(t)),\qquad s_{c_j}(0)=0$$

output gate部分

$$y_{out_j}(t) = f_{out_j}(z_{out_j}(t)),\qquad z_{out_j}(t) = \sum_m{w_{ {out_j}m}y_m(t-1)}$$

上面提到的是LSTM的memory ceil的部分，相当于神经网络的hidden unit，没有谈到输入层和输出层。关于输入层x，以上公式无需特殊变动， 只需要把x并入y(t-1)即可，即$y(t-1) = < y(t-1),x > $ 公式不需要做额外变动，对于输出层需要在隐含层的基础上添加额外的一层：

$$y_{k}(t) = f_{k}(z_{k}(t)),\qquad z_{k}(t) = \sum_m{w_{ {k}m}y_m(t-1)}$$

  forward pass可以看到和普通的神经网络并无特别，只是隐含层设置的精巧罢了。在参数更新的时候，LSTM采用的是truncated back propagation，需要对truncated进行一些额外的说明：truncated是指训练过程中的错误信号到达memory cell的输入处之后就不再继续沿着 时间序列传递下去了（上图方框之外的权重部分），但是在memory cell内部（上图方框内部的部分）并不受truncated影响，依然沿着时间序列 往下传递。注意：这和传统RNN的truncated BPTT算法有着本质的不同，传统的truncated BPTT受到截断的影响无法对较长的时间序列进行 建模，而LSTM的memory cell的内部采用了constant error carrousel机制保证了memory cell可以不会随着时间跨度变长导致gradient vanish或explode， 这部分是不受truncated影响的，是不受建模的时间序列长短影响的，仅是memory cell的输入单元会受到truncated影响。

  truncated BP可以帮助LSTM在参数更新的时候计算可以非常高效，而且实验证明truncated并不会显著影响LSTM的性能，我认为是对于 memory cell的输入部分因为在沿着时间序列进行错误传递的过程中要经过多个gate，这中间一旦有一个gate是关闭的，就会让后面的错误传递不在有 效果，天然形成了truncated的效果，所以直接在第一次经过memory cell的输入处就停止继续传递并不会造成太大影响。

如果还是被这绕圈圈的话弄糊涂了，上面的话翻译成公式就是如下的意思：

$$\frac{\partial {z_{c_j}(t)}}{\partial y_m(t-1)} \overset{t.r.} \approx 0$$ $$\frac{\partial {z_{in_j}(t)}}{\partial y_m(t-1)} \overset{t.r.} \approx 0$$ $$\frac{\partial {z_{\varphi_j}(t)}}{\partial y_m(t-1)} \overset{t.r.} \approx 0$$ $$\frac{\partial {z_{out_j}(t)}}{\partial y_m(t-1)} \overset{t.r.} \approx 0$$

  $\overset{t.r.} \approx$表示truncated之后的结果，表示错误信号在到达在memory cell外面以后不再继续传递下去，为了看得更仔细，可以往前再推一步，可以得到：

$$\frac{\partial {y_{in_j}(t)}}{\partial y_m(t-1)} = {f}'_{in_j} (z_{in_j}(t)) \frac{\partial {z_{in_j}(t)}}{\partial y_m(t-1)} \overset{t.r.} \approx 0$$ $$\frac{\partial {y_{\varphi_j}(t)}}{\partial y_m(t-1)} = {f}'_{\varphi_j} (z_{\varphi_j}(t)) \frac{\partial {z_{\varphi_j}(t)}}{\partial y_m(t-1)} \overset{t.r.} \approx 0$$ $$\frac{\partial {y_{out_j}(t)}}{\partial y_m(t-1)} = {f}'_{out_j} (z_{out_j}(t)) \frac{\partial {z_{out_j}(t)}}{\partial y_m(t-1)} \overset{t.r.} \approx 0$$

对于LSTM的memory ceil的输出$y_{c_j}(t)$有：

$$\frac{\partial {y_{c_j}(t)}}{\partial y_m(t-1)} = \frac{\partial y_{out_j}(t)}{\partial z_{out_j}(t)} \frac{\partial {z_{out_j}(t)}}{\partial y_m(t-1)} + \frac{\partial y_{\varphi_j}(t)}{\partial z_{\varphi_j}(t)} \frac{\partial {z_{\varphi_j}(t)}}{\partial y_m(t-1)} + \frac{\partial y_{in_j}(t)}{\partial z_{in_j}(t)} \frac{\partial {z_{in_j}(t)}}{\partial y_m(t-1)} \overset{t.r.} \approx 0$$

  以上就是对LSTM参数更新算法里面的truncated的解释，有了上面几个式子，下面开始推导参数更新公式，使用梯度下降法有：

$$\Delta w_{lm} = - \alpha \frac{\partial loss}{\partial z_{l}} \frac{\partial z_l}{\partial w_{lm}} = - \alpha \frac{\partial loss}{\partial z_{l}} y_m(t-1) $$

其中$\alpha$是学习步长，loss表示损失函数，这里以均方误差为例，即$loss = (t(t) - y(t))^2$，t(t)表示t时刻的标注数据，y(t)表示t时刻的模型输出。注意：这里的模型输出不是LSTM的$y_c(t)$，$y_c(t)$只是隐含层的输出，模型输出是上面提到过的在隐含层上面另外加的一层$y_k(t)$,首先对输出层的参数进行更新：

\[ \begin{split} \Delta w_{km} &= - \alpha \frac{\partial loss}{\partial z_{k}} y_m(t-1) \\ &=-\alpha e_k(t)f'_k(z_k(t))y_m(t-1) \end{split} \]

其中$e_k(t)$表示$(t_k(t) - y_k(t))$。接下来对out gate进行参数更新：

\[ \begin{split} \Delta w_{out_jm} &= - \alpha \frac{\partial loss}{\partial z_{out_j}} y_m(t-1) \\ &=-\alpha \sum_k \frac{\partial loss}{\partial z_k(t)} \frac{\partial z_k(t)}{\partial z_{out_j}(t)}y_m(t-1) \\ &=-\alpha \sum_k \frac{\partial loss}{\partial z_k(t)} \frac{\partial (w_{kc_j} y_{c_j}(t))}{\partial z_{out_j}(t)}y_m(t-1) \\ &=-\alpha \sum_k \frac{\partial loss}{\partial z_k(t)} \frac{\partial (w_{kc_j} y_{out_j}(t)S_{c_j}(t))}{\partial z_{out_j}(t)}y_m(t-1) \\ &=-\alpha f'_{out_j}(z_{out_j}(t)) S_{c_j}(t) y_m(t-1) \sum_k e_k(t)f'_k(z_k(t)) w_{kc_j} \end{split} \]

在对$w_{c_jm}, w_{in_jm}, w_{\varphi_jm}$进行参数更新前先做一些基础工作，先用$s_{c_j}(t)$对他们分别求导：

\[ \begin{split} \frac{\partial s_{c_j}(t)}{\partial w_{c_jm}} &= \frac{\partial (y_{\varphi_j}(t)s_{c_j}(t-1) + y_{in_j}(t)g(z_(t)))}{\partial w_{c_jm}} \\ &=\frac{\partial s_{c_j}(t-1)}{\partial w_{c_jm}} y_{\varphi_j}(t) + \frac{\partial y_{\varphi_j}(t)}{\partial w_{c_jm}}s_{c_j}(t-1) + \frac{\partial {y_{in_j}(t)}}{\partial w_{c_jm}} g(z_{c_j})(t) + \frac{\partial g(z_(t))}{\partial w_{c_jm}} y_{in_j}(t) \\ &=\frac{\partial s_{c_j}(t-1)}{\partial w_{c_jm}} y_{\varphi_j}(t) + \frac{\partial y_{\varphi_j}(t)}{\partial y_{c_j}(t-1)}\frac{\partial y_{c_j}(t-1)}{\partial w_{c_jm}}s_{c_j}(t-1) + \frac{\partial {y_{in_j}(t)}}{\partial y_{c_j}(t-1)} \frac{\partial {y_{c_j}(t-1)}}{\partial w_{c_jm}}g(z_{c_j})(t) + y_{in_j}(t)g'(z_{c_j}(t))y_m(t-1) \\ & \overset{t.r.} \approx \frac{\partial s_{c_j}(t-1)}{\partial w_{c_jm}} y_{\varphi_j}(t) + 0 + 0 + y_{in_j}(t)g'(z_{c_j}(t))y_m(t-1) \\ &= \frac{\partial s_{c_j}(t-1)}{\partial w_{c_jm}} y_{\varphi_j}(t) + y_{in_j}(t)g'(z_{c_j}(t))y_m(t-1) \end{split} \]

同理可得：

$$\frac{\partial s_{c_j}(t)}{\partial w_{in_jm}} = \frac{\partial s_{c_j}(t-1)}{\partial w_{in_jm}} y_{\varphi_j}(t) + g(z_{c_j}(t))f'_{in_j}(z_{in_j}(t))y_m(t-1)$$ $$\frac{\partial s_{c_j}(t)}{\partial w_{\varphi_jm}} = \frac{\partial s_{c_j}(t-1)}{\partial w_{\varphi_jm}} y_{\varphi_j}(t) + s_{c_j}(t-1)f'_{\varphi_j}(z_{\varphi_j}(t))y_m(t-1)$$

上面三个求导公式里都包含递推公式，即$\frac{\partial s_{c_j}(t)}{\partial w_{lm}}$表示为含有$\frac{\partial s_{c_j}(t-1)}{\partial w_{lm}}$的式子，递推公式的第一项$\frac{\partial s_{c_j}(0)}{\partial w_{lm}}=0$，其中$l \in \{in, c_j, \varphi \}$

接下来看损失函数对$s_{c_j}(t)$的导数：

\[ \begin{split} \frac{\partial loss}{\partial s_{c_j}(t)} &= \sum_k -(t_k(t) - y_k(t))f'_k(z_k(t)) \frac{\partial z_k(t)}{\partial y_{c_j}(t)}\frac{\partial y_{c_j}(t)}{\partial s_{c_j}(t)} \\ &=y_{out_j}(t)\sum_k -e_k(t)f'_k(z_k(t)) w_{kc_j} \end{split} \]

  准备工作做好了，最后针对$in,out,\varphi$的参数进行更新：

$$\Delta w_{c_jm}(t) = -\alpha \frac{\partial loss}{\partial w_{c_jm}(t)} = - \alpha \frac{\partial loss}{\partial s_{c_j}(t)} \frac{\partial s_{c_j}(t)}{\partial w_{c_jm}} $$ $$\Delta w_{in_jm}(t) = -\alpha \frac{\partial loss}{\partial w_{in_jm}(t)} = - \alpha \frac{\partial loss}{\partial s_{c_j}(t)} \frac{\partial s_{c_j}(t)}{\partial w_{in_jm}} $$ $$\Delta w_{out_jm}(t) = -\alpha \frac{\partial loss}{\partial w_{in_jm}(t)} = - \alpha \frac{\partial loss}{\partial s_{c_j}(t)} \frac{\partial s_{c_j}(t)}{\partial w_{out_jm}} $$ 将上面准备工作得到的结果带入，即完成了全部的推导内容